We build models to see what the future will hold and then tailor our actions to what the models tell us. If the models are accurately predictive then great. But sometimes the models are predictive only because we do what they tell us to do. It can be hard to tell the difference.

Self-reinforcing models must recommend actions that make the predictions true and they must appeal to some bias in us that makes us want them to be true. The former is obvious (self-reinforcing models must self-reinforce). The latter is true because we must knowingly ignore evidence the model is incomplete if we are to continue using it. There must be some benefit to it being true that causes us to turn a blind eye to its inadequacies. The benefit may be the actual increase in some good, or it may be a decrease in uncertainty. It may be the continuation of some societal order, or it may simply reinforce something we desperately want to believe about ourselves. This post is about a specific model that we believe because we want to believe there are two ways of existing in our workaday lives: the heroic and the ordinary.

In the innovation economy we have a model that says there are two completely different processes operating at odds with each other. The first process is the everyday, workmanlike creation of ideas that we see at our jobs, that we probably participate in. It is satisfying, important work: making things better one small tweak at a time. But it is different–far different–than the other process, the conjuring out of almost thin air of the big idea, the idea that changes everything because it is flawless and crystalline, dispensing with any possible objections the clock-watching, fault-finding, hierarchy-preserving bureaucrats could gin up. Overcoming the small-minded is the just desserts of the heroic genius who came up with the big idea. "First they ignore you, then they laugh at you, then they fight you, then you win.” Right?

This is a compelling story about a model that seems to reflect what actually happens. I don't think this model is accurate.

If you describe innovation as being either incremental or radical, sustaining or disruptive, it begs the question: is there no medium-sized innovation? Imagine a scale of 1 to 10 that measures technological change (I have no good idea how you would measure this, but it's a thought experiment.) Is sustaining innovation 1–5 and disruptive innovation 9 or 10? Are there no changes of size 6–8? Why would this be? If there aren't, does this imply a specific threshold of human stubbornness regardless of group size? Or is it related to group size or amount of work done on a theory, etc.? If this is so, wouldn't the threshold of revolution change based on these factors? And if so, wouldn't what constituted normal science in one context seem like revolution in another, and vice-versa?

With commercial technological innovation we can often measure a new technology's impact: if a technology is created to improve the throughput of a factory, we can measure the factory's productivity change. What does the data show? Here's a chart I used to illustrate the size of technological change in a previous post. This is real data on the productivity of a container glass factory showing improvements due to technological change.

In that post I used the diagram to show the difference between incremental and radical innovation. Because you can see the qualitative difference between the big changes and the small changes. Can't you?

Here are the size of those changes, rank-ordered. 

Looked at this way, it does not seem like there are big changes and small changes and nothing in-between: there is a lot of 'in-between'. The size of improvements seem almost...power-law-ish.

The 'power-law' curve here is $y=k/x$ where $x$ is the rank and $k$ is a constant. This formulation is called Zipf's Law: the frequency of an item in some systems is inversely proportional to its rank. Zipf found this relationship in written documents, where the frequency of a word is inversely proportional to its frequency  rank. That is, the second most frequent word appears half as often as the most frequent, the third most frequent appears one third as frequently, etc. Zipf's Law is the discrete analogue of a power law.^[1] 

If the impact of innovations followed a power-law distribution, that would explain a lot. Power laws often seem like a two process distribution because we notice the small outcomes (frequent!) and we notice the really big outcomes (really big!). Our instincts tell us to expect outcomes to be more Gaussian but the probability of a power law outcome is higher than a Gaussian in both the tail and in the head of the distribution. We'd expect people to be underwhelmed by the middle of the distribution.^[2] 

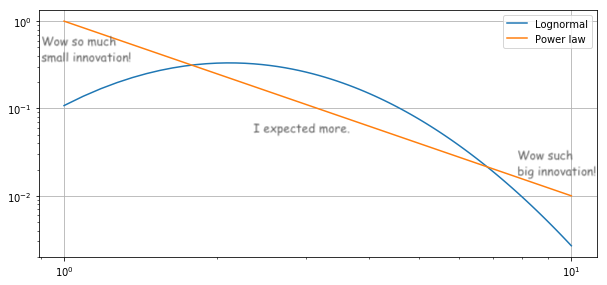
One widely accepted model of technological innovation could easily lead to power-law outcomes. Brian Arthur, in his The Nature of Technology, says that every technology is either a fundamental discovery or an amalgamation of other technologies. Most new technology comes about by combining existing technologies in a new way. For instance, the microprocessor was invented by combining the integrated circuit with a Von Neumann computer architecture. The integrated circuit was a combination of transistor-transistor logic with single-wafer silicon lithography. And so on, down to the more fundamental phenomena of quantum physics and Boolean algebra (and beyond, but you get the picture).

Modularization allows different groups to work on different pieces of the technology. This is a far more efficient way to work. If one group improves semiconductor lithography, for instance, the microprocessor can be made more functional without needing to change every other part. Aspects of modularity allow parallel development. These developments come at unpredictable intervals, in general, but the improvement of the whole technology increases when any of its constituent technologies improve.

Modularization also means that each of the modularized technologies can be used in many places. This allows the development group of each tech to amortize the cost of the development over many customers, resulting in more resources being thrown at the problems and so faster progress on them. It also means that when a technology is improved, all of the technologies that incorporate it can improve.

Think of this as a tree. An idealized tree is below. Each node is a technology. Each technology is comprised of the ones below it, until you reach a fundamental technology at the root of the tree.

This tree-like structure is perhaps not so different from scientific ideas, each theory built on more fundamental theories. 

The impact of a change in a given technology depends on how deep it is in the tree. If the change happens to be in level 4 of the above tree, the only effect is on the technology that changed...no other technology relies on it. We will call this an impact of 1. If it is in level 3, it affects the technology that changed and those immediately above it, that rely on it, for a total impact of 4.

Generally, if the tech change is in level $i$ of a tree with $\ell$ levels where each node branches into $b$ nodes above it then the impact is

                                             $m_i=\sum _{j=1}^{\ell -i+1}{b}^{j-1}=\frac{b^{\ell -i+1}-1}{b-1}$

where $m_i$ is the impact of a change in level $i$.

The interesting thing to know would be the probability distribution of possible impacts, given a change in a randomly selected tech in the tree.

We know the impact of a change in a tech in level $i$, and the probability of selecting a tech in level $i$ is the number of techs in level i / number of techs in the tree.

                                             $p_i=b^{i-1}/\sum _{j=1}^{\ell }{b}^{j-1}=\frac{b^{i-1}(b-1)}{b^{\ell }-1}$

So with probability $p_i$ there is impact $m_i$. This isn't quite what we want, so rewrite it as the probability of a specific impact, m:

                                             $P(M=m=\frac{b^{\ell -i+1}-1}{b-1})=\frac{b^{i-1}(b-1)}{b^{\ell }-1}$

Rearranging $m=\frac{b^{\ell -i+1}-1}{b-1}$, we get $b^i=\frac{b^{\ell +1}}{m(b-1)+1}$ so

                                             $P(M=m)=\frac{b^{\ell }(b-1)}{\left(m\right(b-1)+1)(b^{\ell }-1)}=\frac{b}{(m+\frac{1}{b-1})(1-\frac{1}{b^{\ell }})}$,

where $m\in [\frac{b^j-1}{b-1},j=\mathrm{1..}\ell ]$.

Note that as either $b$ or $\ell$ gets large, this curve begins to approximate a Zipf distribution. 

                                             $P(M=m)\approx 1/m$

Here is a chart of the probability distribution of impact for the above tech tree, compared to a power-law (ie. Zipf) distribution.

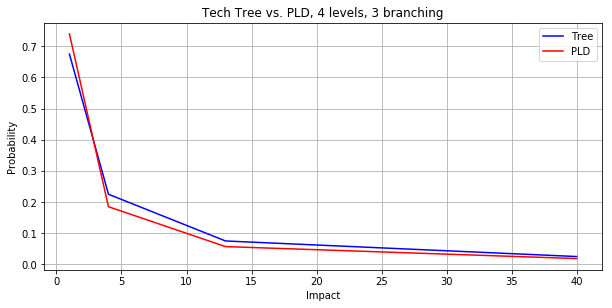
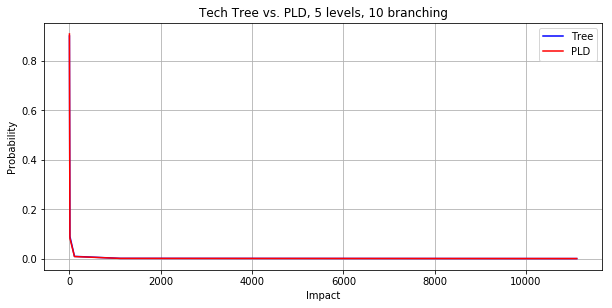
And here is the distribution for a tree that has more levels and a higher branching factor. It is indistinguishable from the power-law distribution.

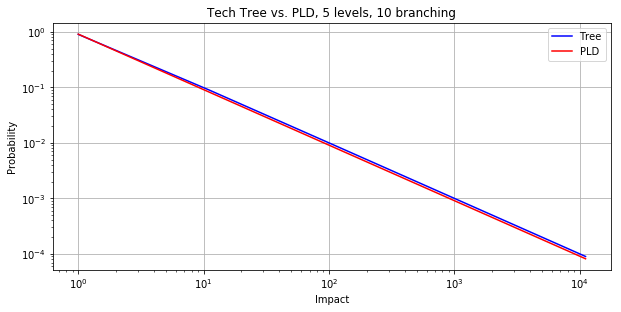
This is the same but on a log-log chart so you can see that it is indeed extremely similar to a power-law distribution.

We can also figure out the average impact of a change in a random tech:

$$\begin{array}{cc}\overline{m}=\sum _{i=1}^{\ell }{m}_i{p}_i& =\sum _{j=1}^{\ell }(\frac{b^{\ell -i+1}-1}{b-1})(\frac{b^{i-1}(b-1)}{b^{\ell }-1})\\ & =\sum _{j=1}^{\ell }\frac{b^{\ell }-b^{i-1}}{b^{\ell }-1}=\ell \frac{b^{\ell }}{b^{\ell }-1}-\frac{1}{b-1}\end{array}$$

As b or $\ell$ gets large, this quickly converges to $\ell$, so $\overline{m}\approx \ell$.

If innovation outcomes are power-law distributed then there aren't really two processes at all, it just seems that way. Clay Christensen, not to mention Kuhn, might have been seriously misreading the situation. It may seem like change faces resistance until it is big enough that the resistance can be swept away, but the truth may be that every change faces resistance and every change must sweep it aside, no matter if the change is tiny, medium-sized, or large. We just tend to see the high frequency of small changes and the large impact of the unusual big changes.

This is a model, of course, and it has many failings. One is that it assumes a regular tree. I believe this to be a small problem in the scheme of things for some fairly intuitive reasons. But intuitions can be wrong so more work needs to be done. A larger problem is the assumption that if there is a change at one level then the changes in the levels above just happen automatically. This is obviously not true: an innovation in lithography may allow innovations in semiconductor manufacturing and then in microprocessors, but somebody has to do that work too. And much of that work is also innovation in itself.

And anyway, what does it matter?

I think it does, both in science and in technology. In technology the very widespread belief that there should be two processes leads people to set up two separate processes. You have big corporations setting up their innovation labs and hiring innovation consultants to get change agents to whiteboard brainstormed intrapreneurship things. But they don't churn out big ideas or even medium-sized ideas because the process is not set up to find those. And if it doesn't, it must implicitly filter them out. If you take a single process and break it into two processes and only use the first part, you do that by censoring the second part. People talk about companies like Apple and Amazon having something special because they still have big ideas. Maybe they're not doing something special, maybe they're just not doing something stupid. In the land of the blind and all that. Walk away from the blue ocean strategy tweaking and look to innovate deeper in the fundamentals of what you do.

As for science, here's an interesting drawing from a paper by Jay Bhattacharya and Mikko Packalen,^[3] that Jason Crawford talked about a while back.

My model assumes that the chance of an innovation at a given level depends on how many places there are to innovate at that level. If you look at the tree you see that there are only a few as you get near the root and many as you get closer to the leaves. This, then, implicitly assumes a somewhat even distribution of innovators (such as, say, scientists) at the various levels, kind of like in the left-hand drawing above. But what happens if innovation effort is moved from being evenly distributed to focusing on closer-to-the leaf innovations, as in the right-hand drawing?

Now, this migration makes a certain amount of sense: the innovations that can be used most widely are the ones at the leaves. An improvement in semiconductor lithography has a limited audience, whereas a smartphone that uses an improved microprocessor has a very large and visible audience. It is also more likely that there will be a breakthrough innovation at the leaves because there are more breakthroughs to be had. If you are a scientist being judged based on quantity of breakthroughs rather than importance of breakthroughs you would be motivated to work near the leaves. And even if you were judged on both, the mean time to a breakthrough near the root would be much higher than near the leaves.

Take Einstein, who worked near the root. He had, for the sake of argument, six major near-root discoveries in his life (The photoelectric effect, on Brownian motion, special relativity, the equivalence of mass and energy, general relativity, and the EPR paradox. Much of his later work was exploring the implications of general relativity, so I'm considering it less root-like. You may strenuously disagree with my characterization of his work, I get that. I'm not an Einstein expert.) The first four of these he published on when he was 26. Later in his life, when he returned to root-level work trying to unify the forces, he made very little progress. Now imagine he worked on force-unification when he was 26, saving the other work for later: he probably would have spent his life working in the patent office and none of his important work would gotten done (at least by him.) His early success gave him the ability to do the work he wanted to for the rest of his life. Now imagine you are a promising young scientist who does not consider themselves an Einstein. What work would you concentrate on first to be sure you got tenure and so had the opportunity to do whatever work you wanted? Definitely not work at the root.

But work at the root lays the basis for work closer to the leaves. If no one does the root work, or not much root work gets done then the work at the leaves will eventually sputter out. Somebody has to do that work, even if it rarely leads to glory.

Also, the work at the root has a disproportionate impact when it is successful. We can calculate the average impact if work is only done in the top j layers of the tree. Rather than doing the math, we can just note that the top j layers are repeated copies of trees with j layers, so the average impact across these smaller, identical trees is the average impact of a tree with j layers, or $\overline{m}\approx j$.

Although we don't really know what the actual tree looks like, what the b and $\ell$ are, we can say that if most of the work is focused in the top half of the tree then the impact of the average scientific innovation is cut in half. And this is before the work at the leaves wanes because there is no innovation at the deeper layers. That is, if scientists focus on closer-to-the-leaf research then there is the double whammy of that work having intrinsically less impact on average and of innovations becoming less and less likely because no changes are bubbling up from below. Bhattacharya and Packalen propose a different model (involving work over time) but the models are analogous: their model shows work being concentrated in the second half of the innovation cycle, while mine sees that as being in the top half of the tree.^[4]

At some point the only researchers having any impact at all will be the few near the root. And I suppose when others eventually notice this the imbalance will swing the other way. But if this is predictable, why wait? At a time when the importance of scientific progress has become starkly evident, can we afford to milk past discoveries for only a fraction of the impact we could get if we incentivized fundamental research? If there was a chance Einstein was going to have his most important ideas when he was 56 instead of 26, wouldn't we still want to have given him the chance to do so? Just so, we should be celebrating researchers doing the hard and so-often unrewarding work deep in the tree even if we aren't sure anything will come of it. If you only reward innovators for results, the results you get will be anemic. If you support them for potential, your results might be spectacular.

1. ^{^}

   Not a power-law distribution! To get from ranked order, where $y=x^{-b}$ to power law distribution, you basically have to swap the x and y axes so that $x=y^{-1/b}$. Since this is the CDF, you add one to the (negative of the) exponent to get the alpha of the PDF. $Alpha=1+\left(1/b\right)$. In the case of Zipf's Law, where b=1, alpha=2. For more detail see Adamic, LA, "Zipf, Power-laws, and Pareto - a ranking tutorial

2. ^{^}

   Though neither pursues the idea in any depth, the idea that power law distributed breakthroughs may seem bimodal was mentioned briefly in Sornette, D. (2008). Nurturing Breakthroughs: Lessons from Complexity Theory. J Econ Interact Coord, 3:165-181. Sornette credits the idea to Buchanan, M. (1996). Measuring Science Revolutions. Nature, Vol. 384, Iss. 6607, p. 325.

3. ^{^}

   Bhattacharya, J and M Packalen "Stagnation and Scientific Incentives", NATIONAL BUREAU OF ECONOMIC RESEARCH, Working Paper 26752, February 2020, p. 22.

4. ^{^}

   I disagree with their model. It is akin to the linear model of innovation in technology, where a new idea leads to downstream new ideas. This is not really what happens. Sometimes a new idea occurs downstream and then works its way back upstream, etc. But that's off-topic here.