In the most important century blog post series, Open Philanthropy’s co-CEO Holden Karnofsky says that there are basically three potential future trajectories for civilization:
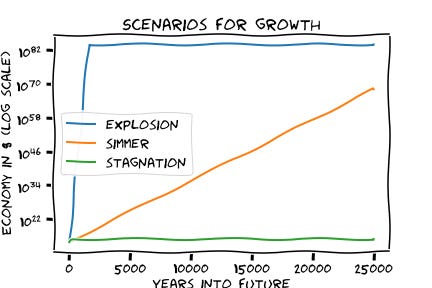
The world can't just keep growing at this rate indefinitely. We should be ready for other possibilities: stagnation (growth slows or ends), explosion (growth accelerates even more, before hitting its limits), and collapse (some disaster levels the economy).
There’s a fourth possibility worth taking seriously: the simmer scenario, where growth slows down, but stays consistent and significant for the foreseeable future.
Here, growth slows to 0.2 - 0.5% a year (from today’s 2% annual growth rate) for the duration of time we are stuck in the Milky Way (25,000 years). After that, we grow as fast as we can expand to other galaxies.
In this post, I will argue that:
The simmer scenario is plausible and worth taking seriously.
In the simmer scenario, lock-in becomes much less likely. Even if economic growth slows to 0.2%, lots of stuff is changing all the time, and no century ends up being especially important.
To be clear, I’m not defending the following claim:
The simmer scenario is more likely that explosion, stagnation, and collapse. Making this argument would require you to resolve a whole bunch of specific questions that are beyond the means of a single post - about AI’s arrival date and power, the amount of energy and compute we can extract from our solar system and galaxy, how fast we can expect innovation to occur in the future, and much more.
Billions of Years of Growth
Holden Karnofsky argues that this can’t go on:
Let's say the world economy is currently getting 2% bigger each year. This implies that the economy would be doubling in size about every 35 years.
If this holds up, then 8200 years from now, the economy would be about 3*10^70 times its current size.
There are likely fewer than 10^70 atoms in our galaxy, which we would not be able to travel beyond within the 8200-year time frame.
So if the economy were 3*10^70 times as big as today's, and could only make use of 10^70 (or fewer) atoms, we'd need to be sustaining multiple economies as big as today's entire world economy per atom.
I agree with Holden that 2% growth for the next 8,200 seems unfeasibly high. But one of compound growth’s most counterintuitive features is that small changes in the growth rate can have a tremendous impact over the long run. Tyler Cowen has a neat example of this in Stubborn Attachments:
redo U.S. history, but assume the country’s economy had grown one percentage point less each year between 1870 and 1990. In that scenario, the United States of 1990 would be no richer than the Mexico of 1990.
The nearest galaxy to the Milky Way is 25,000 light years away. So we don’t need indefinite growth just from the resources in the Milky Way - we only need to sustain some level of growth until we can access and exploit the resources of other galaxies. So how much growth can we get out of the Milky Way during the timespan in which we’re stuck here?
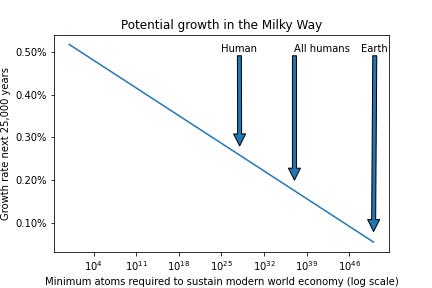
Suppose you think that we can sustain one modern-world-economy per atom in the Milky Way (in the next post, I’ll talk about why this may be more plausible that you think). If this is the physical limit of growth, then we can sustain more than .5% growth annually for the next 25,000 years. That’s a full quarter of the seemingly absurd 2% growth figure that Holden uses in his thought experiment.
But suppose you think that one world economy per atom would be ridiculous, and that it would take a whole human body’s worth of matter (10^28 atoms) to maximally compress than much economic value. Remember how I said that small differences in growth rates can have a large impact on the end result over a long enough period of compounding? Well, here’s a great example. Even at this density, you could have .26% growth for the next 25,000 years. That’s only an order of magnitude lower than present day growth rates!
The cool thing is that you can drastically increase what you expect the maximum density of economic value to be, and the growth will still stay within an order of magnitude of .2%. If you think it would take all the atoms in every human body on Earth to sustain one current world sized economy, then you can still have .17% growth a year for the next 25,000 years.
Or consider the pathological case. Suppose you thought that we had achieved peak GDP per atom right now - that is, on average, the amount of atoms in the world could only sustain our current level of GDP. Even then, making the rest of the galaxy just as productive as our planet currently is atom-for-atom would still give you 6 basis points of growth a year, which is more than half the growth rate we experienced in the agricultural era (i.e. most of the time that civilization has been around).
The following graph shows you what growth rate is possible based on how many atoms it takes to sustain a current world-sized economy. Keep in mind the x-axis is in log scale. Here’s the code and here’s the derivation.
After 25,000, we can expand into the rest of the galaxies in the local group and make them as economically efficient as we’ve made the Milky Way. Which means we can still experience economic growth. This cloud of maximum productivity will expand as we travel farther and farther away, meaning the size of the economy will be proportional to the volume of the sphere which circumscribes our influence. So the size of the economy will just be some constant k[1] * time^3[2].
That’s a polynomial function, which means it cannot keep up with the exponential growth we have relied on in recent history. But it’s still pretty good! Ask any programmer how fast the compute required to execute an O(N^3) algorithm grows.
In reality, we’re probably being too pessimistic by assuming the best we will be able to do after we make it to other galaxies is just to convert them into this GDPium which has a fixed maximum value. The principle of specialization tells us that as more of the universe is controlled by economic agents trying to trade, we’ll see increasing gains from economies of scale and accumulation of know-how. Of course, we’re not accounting for transaction costs here, and light speed is a hell of a transaction cost. But if the increasing returns never stop, exponential growth may be possible in perpetuity.
So we have a plausible model of 0.2-0.5% exponential economic growth for the next 25,000 years (!) until we can escape the Milky Way, and then polynomial growth for billions of years until we reach the edges of the affectable universe. That’s a lot of growth!
To be clear, 0.2% growth is only a tenth of present day growth rates, so clearly we’ll be forced to migrate to a slower post-industrial growth regime. In that sense, “this” - 2% growth - really can’t go on much longer. But in a world with 0.2% growth, “this” meaning change, improvement and turnover - can go on indefinitely, which would reduce the risk of lock-in.
Lock-in is Unlikely in the Simmer Scenario
Holden writes:
It's possible, for reasons outlined here, that whatever the main force in world events is (perhaps digital people, misaligned AI, or something else) will create highly stable civilizations with "locked in" values, which populate our entire galaxy for billions of years to come. If enough of that "locking in" happens this century, that could make it the most important century of all time for all intelligent life in our galaxy.
If the simmer scenario (.2% growth a year for 25,000 years) represents our future growth trajectory, then a stable locked-in civilization becomes implausible. This level of growth means that over the course of centuries and millennia, lots of things are changing. Some examples:
At our current growth rate of 2%, a general purpose technology as important and revolutionary as the computer may come around every 50 years[3]. If the growth rate slows to .2% for the coming millennia, then that means we should expect a technology as impactful as the computer every 500 years. That means that over the next 25,000 years in which we’re stuck in our galaxy, there will be over 50 new technologies developed that are as revolutionary as the computer.
Under a .2% growth rate, the doubling time of the economy goes from 35 years now to about 350 years. But on a galactic time scale, that’s nothing! That’s as long as it takes light to travel 1/285ths of the Milky Way. So the economy would be doubling faster than it would take light can access just a tiny tiny fraction of our galaxy.
Does that sound like a civilization which is stable, stagnant, and locked-in? The development of the printing press resulted in wars, revolutions, religions, political movements, and further scientific and technological advances which have completely remade the world. In the simmer scenario, a technology as fundamental as that is being developed every 500 years for the remainder of our time in the galaxy. In this scenario, no century ends up having extraordinarily important technological changes in the grand scheme of things.
You could argue that lock-in is still compatible with the simmer scenario - maybe we develop a giga-super-human AI that kills all humans and manufactures thousands of years of growth by converting the galaxy into paperclips. But if AIs end up being so much more powerful than humans that they can kill us all or permanently and destructively change the trajectory of civilization, then they could also significantly raise growth rates, which would mean we’re in the explosion scenario, not the simmer scenario.
To reiterate from the introduction, I’m not arguing that the simmer scenario is more likely than explosion - only that it is a plausible alternative worth considering further.
In the next post in this series, I’ll discuss why I think Holden is wrong about the limits of growth.
